Sigmoid function is an activation function that gives value in the range of 0 to 1. Values very much less than 0 gives activation value close to 0 and values very much greater than 0 gives activation value close to 1.
It can be expressed mathematically as:
$$ \sigma (x) = \cfrac {1} {1+{e}^{-x}}$$
Sigmoid function is used as the final activation function when we need to find if something is True. It gives the probability that something is True or False as the truth we define. For example, if we are to find if the given picture is cat, we may use sigmoid function as the final activating function. But if we are to do multi-class problem, shall we use sigmoid function for all the classes or is there any other function?
Softmax function is widely used for multi-class classification problem. But how does it compare with sigmoid function applied to all the classes?
It turns out that having sigmoid function for all the classes is same as having softmax function. It does not matter which activation function we would use. We would be doing same thing. Training using either of the functions is mathematically identical. Let's see it how for single-class classification problem.
We employ sigmoid function giving result the probability of some picture being a cat. That can be said as the two class classification problem having labels as:
1) Being a cat
2) Not being a cat
So, using sigmoid function as final activation function, we would get equivalent two-classes final activation as:
$$ \left( {a}_{1} \quad {a}_{2}\right)=\left( \cfrac {1} {1 + {e}^{-{z}_{1}}} \quad \cfrac {{e}^{-{z}_{1}}} {1+{e}^{-{z}_{1}}} \right)\quad \dots \quad (1)$$
Note that we got ${a}_{2}$ by subtracting ${a}_{1}$ from $1$.
That is same as applying sigmoid function on each classes output. In that case we would get:
$$ \left( { a }_{ 1 }\quad { a }_{ 2 } \right) =\left( \cfrac { 1 }{ 1+{ e }^{ -{ z }_{ 1 } } } \quad \cfrac { 1 }{ 1+{ e }^{ -{ z }_{ 2 } } } \right) $$
Equating the value of ${a}_{2}$ and simplifying, we would get:
$$ {z}_{1}=-{z}_{2}\quad\dots\quad(2)$$
Putting $(2)$ into $(1)$,
$$\left( {a}_{1} \quad {a}_{2}\right)=\left( \cfrac {1} {1 + {e}^{-{z}_{1}}} \quad \cfrac {{e}^{{z}_{2}}} {1+{e}^{{z}_{2}}} \right)$$
Now, multiplying ${a}_{1}$ by ${e}^{\frac{{z}_1} {2}}$ and ${a}_{2}$ by ${e}^{-\frac{{z}_2} {2}}$ in both numerator and denominator, we would have:
$$\left( {a}_{1} \quad {a}_{2}\right)=\left( \cfrac {{e}^{\frac{{z}_1} {2}}} {{e}^{\frac{{z}_1} {2}} + {e}^{\frac{-{z}_{1}} {2}}} \quad \cfrac {{e}^{\frac{{z}_{2}}{2}}} {{e}^{-\frac{{z}_{2}}{2}}+{e}^{\frac{{z}_{2}}{2}}} \right)\quad\dots\quad(3)$$
Using $(2)$ in $(3)$,
$$\left( {a}_{1} \quad {a}_{2}\right)=\left( \cfrac {{e}^{\frac{{z}_1} {2}}} {{e}^{\frac{{z}_1} {2}} + {e}^{\frac{{z}_{2}} {2}}} \quad \cfrac {{e}^{\frac{{z}_{2}}{2}}} {{e}^{\frac{{z}_{1}}{2}}+{e}^{\frac{{z}_{2}}{2}}} \right)\quad\dots\quad(3)$$
$(3)$ is same as using final activation as softmax function where the $z$ values are $\frac{{z}_{1}}{2}$ and $\frac{{z}_{2}}{2}$. It is no different than using softmax function on the $z$ values ${z}_{1}$ and ${z}_{2}$ as the two methods differ in just scaling of $z$ values.
So, training using sigmoid function for single class classification as final activation function is just a case for training using softmax function using two classes. We can see the same true for more than two classes classification cases too.
It can be expressed mathematically as:
$$ \sigma (x) = \cfrac {1} {1+{e}^{-x}}$$
Sigmoid function is used as the final activation function when we need to find if something is True. It gives the probability that something is True or False as the truth we define. For example, if we are to find if the given picture is cat, we may use sigmoid function as the final activating function. But if we are to do multi-class problem, shall we use sigmoid function for all the classes or is there any other function?
Softmax function is widely used for multi-class classification problem. But how does it compare with sigmoid function applied to all the classes?
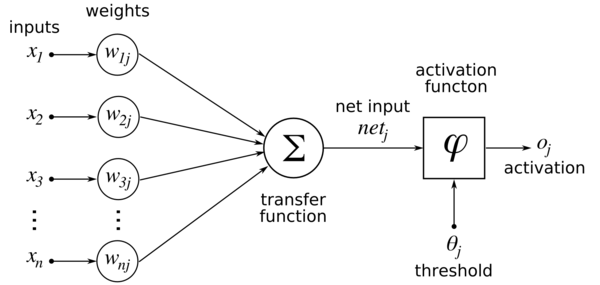 |
| Block diagram of logistic regression |
It turns out that having sigmoid function for all the classes is same as having softmax function. It does not matter which activation function we would use. We would be doing same thing. Training using either of the functions is mathematically identical. Let's see it how for single-class classification problem.
We employ sigmoid function giving result the probability of some picture being a cat. That can be said as the two class classification problem having labels as:
1) Being a cat
2) Not being a cat
So, using sigmoid function as final activation function, we would get equivalent two-classes final activation as:
$$ \left( {a}_{1} \quad {a}_{2}\right)=\left( \cfrac {1} {1 + {e}^{-{z}_{1}}} \quad \cfrac {{e}^{-{z}_{1}}} {1+{e}^{-{z}_{1}}} \right)\quad \dots \quad (1)$$
Note that we got ${a}_{2}$ by subtracting ${a}_{1}$ from $1$.
That is same as applying sigmoid function on each classes output. In that case we would get:
$$ \left( { a }_{ 1 }\quad { a }_{ 2 } \right) =\left( \cfrac { 1 }{ 1+{ e }^{ -{ z }_{ 1 } } } \quad \cfrac { 1 }{ 1+{ e }^{ -{ z }_{ 2 } } } \right) $$
Equating the value of ${a}_{2}$ and simplifying, we would get:
$$ {z}_{1}=-{z}_{2}\quad\dots\quad(2)$$
Putting $(2)$ into $(1)$,
$$\left( {a}_{1} \quad {a}_{2}\right)=\left( \cfrac {1} {1 + {e}^{-{z}_{1}}} \quad \cfrac {{e}^{{z}_{2}}} {1+{e}^{{z}_{2}}} \right)$$
Now, multiplying ${a}_{1}$ by ${e}^{\frac{{z}_1} {2}}$ and ${a}_{2}$ by ${e}^{-\frac{{z}_2} {2}}$ in both numerator and denominator, we would have:
$$\left( {a}_{1} \quad {a}_{2}\right)=\left( \cfrac {{e}^{\frac{{z}_1} {2}}} {{e}^{\frac{{z}_1} {2}} + {e}^{\frac{-{z}_{1}} {2}}} \quad \cfrac {{e}^{\frac{{z}_{2}}{2}}} {{e}^{-\frac{{z}_{2}}{2}}+{e}^{\frac{{z}_{2}}{2}}} \right)\quad\dots\quad(3)$$
Using $(2)$ in $(3)$,
$$\left( {a}_{1} \quad {a}_{2}\right)=\left( \cfrac {{e}^{\frac{{z}_1} {2}}} {{e}^{\frac{{z}_1} {2}} + {e}^{\frac{{z}_{2}} {2}}} \quad \cfrac {{e}^{\frac{{z}_{2}}{2}}} {{e}^{\frac{{z}_{1}}{2}}+{e}^{\frac{{z}_{2}}{2}}} \right)\quad\dots\quad(3)$$
$(3)$ is same as using final activation as softmax function where the $z$ values are $\frac{{z}_{1}}{2}$ and $\frac{{z}_{2}}{2}$. It is no different than using softmax function on the $z$ values ${z}_{1}$ and ${z}_{2}$ as the two methods differ in just scaling of $z$ values.
So, training using sigmoid function for single class classification as final activation function is just a case for training using softmax function using two classes. We can see the same true for more than two classes classification cases too.